ベクトルは向きと長さを表現する方法である。

　移動の方向と速度や、力の方向と大きさなどを図や数式で表現できる。
　
　点 p ( x1, y1, z1 ) から、点 q ( x2, y2, z2 ) へのベクトルは、
　　　u ( x2 - x1, y2 - y1, z2 - z1 )
　となる。
　
　点 q から 点 p へのベクトルは、
　　　v ( x1 - x2, y1 - y2, z1 - z2 )
　となる。
　
　u と v は、逆向きで同じ長さのベクトルとなっている。
　
　逆算すると、ベクトルと一方の座標から、
　もう一方の座標を求めることができる。

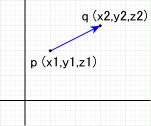
　点 p ( x1, y1, z1 ) と、点 q ( x2, y2, z2 ) の間の距離 Len は、
　
　　　Len = sqrt ((x2-x1) * (x2-x1) + (y2-y1) * (y2-y1) + (z2-z1) * (z2-z1));
　
　となる。
　
　これは、点 p から 点 q へのベクトル、または点 q から 点 p へのベクトルの長さでもある。
　
　　　float Len = D3DXVec3Length (&D3DXVECTOR3(x2-x1, y2-y1, z2-z1));
　
　でも同じである。

DirectX では、ベクトルから単位ベクトルを求める事を正規化と呼んでいる。
単位ベクトルとは、長さ１のベクトルのことである。
ベクトル p(a,b,c) の単位ベクトル q(x,y,z) は、

x = a / sqrt (a * a + b * b + c * c);
y = b / sqrt (a * a + b * b + c * c);
z = c / sqrt (a * a + b * b + c * c);

で求める事ができる。

D3DXVECTOR3 q;
D3DXVec3Normalize (&q, &D3DXVECTOR3(a, b, c));

でも同じである。

角度の単位には、度（degree,deg）とラジアン（radian,rad）があり、以下の関係がある。

deg = rad * 180 / PI
（PI は円周率）

サインは単位ベクトルの垂直方向の成分であり、コサインは水平方向の成分である。
成分とは、ベクトルを垂直と水平の各方向に分解した時のそれぞれの長さの事だ。
そのため、
sinθ * sinθ + cosθ * cosθ = 1
となる。

x軸から角度 θ（rad）傾いた単位ベクトルの位置に移動したいときは、x軸方向に cosθ、y軸方向に sinθ 移動すればよい。
長さが L のベクトルの場合は、それぞれ、L * cosθ、L * sinθ となる。

当サイトのサンプルプログラムは、ｙ軸からθ（rad）回転するため、x軸方向に sinθ、y軸方向に cosθ 移動する。

学校では、sin, cos, tan は右図のようにして覚えると教わる。
sinθ = c / a
cosθ = b / a
tanθ = c / b

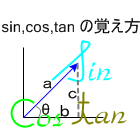
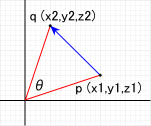
　点 p ( x1, y1, z1 ) をＺ軸を中心にθ（ラジアン） 回転した 点 q ( x2, y2, z2 )は、
　
x2 = x1 * cos(θ) - y1 * sin(θ);
y2 = x1 * sin(θ) + y1 * cos(θ);
z2 = z1;
　
　Ｚ軸を中心に -θ 回転したときは、
　
x2 = x1 * cos(θ) + y1 * sin(θ);
y2 = x1 * (- sin(θ)) + y1 * cos(θ);
z2 = z1;
　
　となる。
　行列を使用すると以下のように置き換えられる。

D3DXMATRIX mat;
D3DXVECTOR3 p(x1, y1, z1), q;
D3DXMatrixRotationZ(&mat, θ);
D3DXVec3TransformCoord(&q, &p, &mat);

　
　原点以外の点を中心として回転する場合は、
　その中心点を原点に移動した後、
　回転し、元の位置に移動する。
　
　点 p ( x1, y1, z1 ) を 点 r ( x3, y3, z3 ) を中心に
　θx (X軸回り), θy (Y軸回り), θz (Z軸回り)（単位はラジアン）
　回転した 点 q ( x2, y2, z2 )は、
　
xx = x1 - x3;
yy = y1 - y3;
zz = z1 - z3;
x2 = xx;
y2 = yy * cos(θx) - zz * sin(θx);
z2 = yy * sin(θx) + zz * cos(θx);
xx = x2 * cos(θy) - z2 * sin(θy);
yy = y2;
zz = x2 * sin(θy) + z2 * cos(θy);
x2 = xx * cos(θz) - yy * sin(θz);
y2 = xx * sin(θz) + yy * cos(θz);
z2 = zz;
x2 += x3;
y2 += y3;
z2 += z3;

　となる。
　回転は原点を中心に行った方が分かりやすいので
　このようにする。

　行列を使用すると以下のように置き換えられる。
　行列は、計算が速い、実行順序を考慮しなくて良い
　といった利点がある。
　例えば、腕の場合、上の方法では指→手首→肘の順に実行する
　必要がある。行列は、どこから実行しても結果は同じになる。
　ただし、行列を掛け合わせる順序は指→手首→肘の順にする。

D3DXMATRIX mat,matT1,matT2,matRX,matRY,matRZ;
D3DXVECTOR3 p(x1, y1, z1), q;
D3DXMatrixTranslation(&matT1, -x3, -y3, -z3);
D3DXMatrixTranslation(&matT2, x3, y3, z3);
D3DXMatrixRotationX(&matRX, θx);
D3DXMatrixRotationY(&matRY, θy);
D3DXMatrixRotationZ(&matRZ, θz);
mat = matT1 * matRX * matRY * matRZ * matT2;
D3DXVec3TransformCoord(&q, &p, &mat);

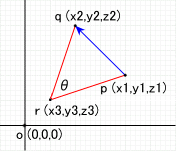
　座標 p0(x0,y0,z0), p1(x1,y1,z1), p2(x2,y2,z2)で
　構成される三角形の面の法線ベクトル n(n_x,n_y,n_z)
　
　　float n_x,n_y,n_z,len;

　　n_x = (y1-y0)*(z2-z0)-(z1-z0)*(y2-y0);
　　n_y = (z1-z0)*(x2-x0)-(x1-x0)*(z2-z0);
　　n_z = (x1-x0)*(y2-y0)-(y1-y0)*(x2-x0);
　　len = (float)sqrt(n_x*n_x+n_y*n_y+n_z*n_z);
　　if(len != 0.0f){
　　　n_x /= len;
　　　n_y /= len;
　　　n_z /= len;
　　}

　これは、以下のように置き換えられる

　　D3DXVECTOR3 p0(x0,y0,z0), p1(x1,y1,z1), p2(x2,y2,z2);
　　D3DXVECTOR3 u( p1 - p0 );
　　D3DXVECTOR3 v( p2 - p0 );
　　D3DXVECTOR3 n;
　　D3DXVec3Cross( &n, &u, &v );
　　D3DXVec3Normalize( &n, &n );

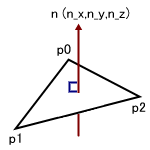
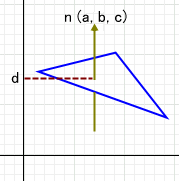
　　法線ベクトルが n(a,b,c)、原点との最短距離が d の面の方程式
　　
　　ax + by + cz + d = 0
　　
　　法線ベクトルがY軸に平行なときは、d は面のY座標になる
　　
　　Direct3D では、以下のようになる。
　　
　　D3DXPLANE plane( a, b, c, d );

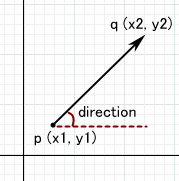
点 p ( x1, y1 ) から、点 q ( x2, y2 ) への向き direction（度）

float direction = (float) atan2(x2 - x1, y2 - y1) * 180 / 3.14f;

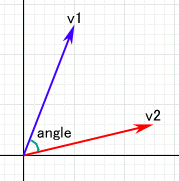
D3DXVECTOR3 v1(x1,y1,z1), v2(x2,y2,z2);
float angle;
angle = (float) acos(D3DXVec3Dot(&v1, &v2)) * 180 / 3.14f;

angle の単位は度。
v1, v2 は単位ベクトルでなくても良い。

ベクトル u( ux, uy, uz ) と v( vx, vy, vz ) の内積は、以下の式で表される

u・v = ux * vx + uy * vy + uz * vz

他には、以下の関係が成り立つ

u・v = |u||v|cosθ

( |u|, |v| は、それぞれのベクトル長 )

もし、u・v が 0 より小さい場合は、u と v の成す角度は鋭角であり、
0 より大きい場合は、鈍角である

内積計算には、D3DXVec3Dot()を使える

ベクトル u( ux, uy, uz ) と v( vx, vy, vz ) の外積は、以下の式で表され、

u×v = ( uy * vz - uz * vy, uz * vx - ux * vz, ux * vy - uy * vx )

u と v が作る面の法線ベクトルを意味する。

ただし、単位ベクトルではない。

Direct3D では、わざわざ単位ベクトルにしなくても良い場合がある。

他には、以下の関係が成り立つ

u×v = - ( v×u )

これは、外積の順番によっては、逆向きの法線ベクトルが得られることを意味する。
2ベクトルの方向によっても、逆向きになる場合がある。

外積計算には、D3DXVec3Cross()を使える。


外積の Z 成分は、2D でも使える。
凸（convex）多角形の頂点の並んでいる方向は、外積の Z 成分が正の場合は右回り、負の場合は左回りになる（左図）。
D3DXVECTOR2 u1(p2.x - p1.x, p2.y - p1.y);
D3DXVECTOR2 v1(p3.x - p2.x, p3.y - p2.y);
float cross_x1 = u1.x * v1.y - u1.y * v1.x;
図の場合は、右回りなので、cross_x1 は正の値になる。

また、ある点が、ベクトルのどちら側にあるかの判定にも使える（右図）。
D3DXVECTOR2 u2(p5.x - p4.x, p5.y - p4.y);
D3DXVECTOR2 v2(p6.x - p4.x, p6.y - p4.y);
float cross_x2 = u2.x * v2.y - u2.y * v2.x;
図の場合は、点 p6 は、ベクトル u2 の右側にあるので、cross_x2 は正の値になる。

例：DX9_Chase2　多角形のクリッピング

行列（マトリックス）は、学校では線形代数の授業で学習する。
行列を使うと頂点座標やベクトルの回転、平行移動、拡大縮小を行うことができる。
行列を使うと処理が速いなどの利点がある。
行列は加減算と乗算ができるが、3D座標変換では乗算を使用する。
また、3D座標変換では 4×4 の行列を使用することが多い。

ベクトル（x1,y1,z1）を変換し、変換後のベクトルを（x2,y2,z2）とする場合を考える。
変換は下図のように行列の乗算を行う。
z1 と z2 の後に 1 を追加するのは、掛ける行列の横方向の数と掛けられる行列の縦方向の数が一致していないと行列の乗算は成り立たないためで、便宜上、そうしなくてはならない。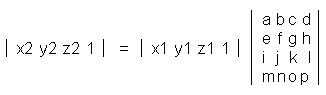

この計算式は実際には以下のようにして求める
x2 = x1 * a + y1 * e + z1 * i + 1 * m
y2 = x1 * b + y1 * f + z1 * j + 1 * n
z2 = x1 * c + y1 * g + z1 * k + 1 * o

下図のように左上からの対角線に 1 が並び、他が 0 の行列を単位行列と呼ぶ。
単位行列は、座標やベクトルに掛けても何も変換が行われない。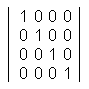


X軸を中心に θ（ラジアン）回転する場合の行列


Y軸を中心に θ（ラジアン）回転する場合の行列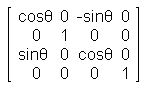


Z軸を中心に θ（ラジアン）回転する場合の行列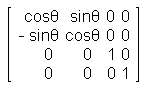


X、Y、Z の各軸方向に 5、6、7、平行移動する場合の行列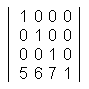


X、Y、Z の各軸方向に 2 倍、3 倍、4 倍、拡大する場合の行列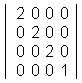


ここでは、ベクトルや座標の行列に掛ける側の行列（回転行列や平行移動行列など）を変換行列と呼ぶことにする。
複数の変換行列を乗算して、1つの変換行列にすることができ、これを行列連結と呼ぶ。
行列連結をすると計算の数を減らすことができ、その結果、ベタで計算するよりも処理速度が向上するのである。
下図は2×2行列の乗算だが、4×4行列も同様である。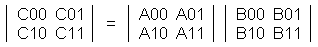

C11 = A11 * B11 + A12 * B21
C12 = A11 * B12 + A12 * B22
C21 = A21 * B11 + A22 * B21
C22 = A21 * B12 + A22 * B22

行列の乗算は、掛け合わせる順番によって結果が異なるので注意する。
具体的には、原点を中心に回転した後、平行移動するということが多い。

Direct3D では、以下のような D3DX 関数が使えるのでこれらの計算を実際にする必要はない。

以下のように、行列のパラメーターを直接指定する方法もある。
例えば、ベクトル v1 を Z 軸を中心に 60 度回転してベクトル v2 を求める場合

D3DXMATRIX matrix;
D3DXVECTOR3 v1(x, y, z), v2;
double angle = 60.0 * 3.14 / 180;
D3DXMatrixIdentity(&matrix);
matrix._11 = (float) cos(angle);
matrix._12 = (float) sin(angle);
matrix._21 = (float)-sin(angle);
matrix._22 = (float) cos(angle);
D3DXVec3TransformCoord(&v2, &v1, &matrix);

2つのモーションを作成した後、それらの中間のモーションを関節の回転角度や平行移動量などを計算することで求めることができる。
これをキーフレームと呼ぶ。
補間の計算式には、y = kx （k は係数） の直線式や、各種の曲線式がある。
曲線式には、エルミート、ベジエ、B-スプラインなどがあるが、DirectX には、エルミート スプライン曲線補間を簡単に行える関数がある。
D3DXVec3CatmullRom 関数は、4つの座標を引数に与えると、2つ目と3つ目の座標の間に作る補間座標を返す。

次のコードを実行すると、v2 と v3 の中間の v5 が返される。
最後の引数は加重係数で、値が小さいほど v2 に近い位置の座標が、大きくなるほど v3 に近い位置の座標が返される。
0.5 の場合は真ん中になる。
例えば、加重係数を、0.25, 0.5, 0.75 でこの関数を3回繰り返せば、間に3つのモーションを作成できる。

D3DXVECTOR2 v1(0,0), v2(0,5), v3(5,5), v4(5,0), v5;
D3DXVec2CatmullRom(&v5, &v1, &v2, &v3, &v4, 0.5f);

これと似たような関数に、D3DXVec2Hermite がある。;
この関数は引数に、v2, v3 の座標とそれぞれの接線ベクトルを指定する。

D3DXVECTOR2 t2, t3;
t2 = v3 - v1;
t3 = v4 - v2;
D3DXVec2Normalize(&t2, &t2);
D3DXVec2Normalize(&t3, &t3);
D3DXVec2Hermite(&v5, &v2, &t2, &v3, &t3, 0.5f);

演算結果がより円に近い、接線ベクトルの長さを変えることで曲がり具合を調整できるという点から、D3DXVec2Hermite の方が使いやすいと思う。
接線ベクトル長が、1 の時、点 v5 は 点 v1 〜 v4 を通る(楕)円上にある。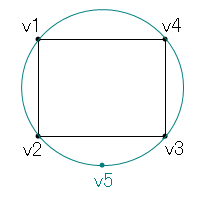


X座標に順番を、Y座標に角度を入れると回転角度も求めることができる。

  int         angle1=0,angle2=90,angle3=180,angle4=270,angle5;
  D3DXVECTOR2 r1,r2,r3,r4,r5;
  D3DXVECTOR2 t2, t3;
  
  r1.x = (float) 1;
  r2.x = (float) 2;
  r3.x = (float) 3;
  r4.x = (float) 4;
  r1.y = (float) angle1;
  r2.y = (float) angle2;
  r3.y = (float) angle3;
  r4.y = (float) angle4;
  // 以下の青文字18行は、角度が小さい方に回転するようにした場合
  if((r3.y - r2.y) >= 180){
    r3.y -= 360;
  }
  else if((r3.y - r2.y) <= -180){
    r2.y -= 360;
  }
  if((r2.y - r1.y) >= 180){
    r1.y += 360;
  }
  else if((r2.y - r1.y) <= -180){
    r1.y -= 360;
  }
  if((r4.y - r3.y) >= 180){
    r4.y -= 360;
  }
  else if((r4.y - r3.y) <= -180){
    r4.y += 360;
  }
  t2 = v3 - v1;
  t3 = v4 - v2;
  D3DXVec2Normalize(&t2, &t2);
  D3DXVec2Normalize(&t3, &t3);
  D3DXVec2Hermite(&r5, &r2, &t2, &r3, &t3, 0.5f);
  angle5 = (int) r5.y;